Category Archives: math

education, home school, home school math, math, modular learning, systems, unschooling

Adventures in Homeschooling: Fun With Arrays

4 Comments

As we transitioned to math activities that were more engaging for my kiddo, I started to notice similarities and patterns. At this point, I was using the book Moebius Noodles as our primary inspiration for math activities. For example, we would have a lot of fun playing around with body symmetry exercises, where one person mirrored the other. We would estimate height by guessing and then building a tower with Duplo blocks. The tower would inevitably collapse, leading to lessons about structure and making a solid base. We played a “program Dad” game where he would direct me around the house by telling me exactly what to do. We found that using a checkerboard tile exercise mat helped a lot. For example, kiddo would tell me to move forward three squares, then turn one square to the right. We played around with grids, working with numbers or drawing items within the shape.

I am a programmer, so playing with grids make me think of arrays. Arrays are used a lot in programming languages as handy data structures. You can use them to store and access objects that you want to interact with in a computer program. When I was learning about arrays in programming, I found simple examples made sense, but when you added more dimensions or started thinking about performance, I struggled. I had trouble with thinking in abstractions. It took a long time to overcome that. The actual concepts, code and mathematics were simple, but my brain struggled to think about something virtual with different dimensions. Similarly, when I started a linear algebra course, I spent too much brain power getting my head wrapped around how arrays were formed, and keeping track of what number was in what row or column. The actual math was often elementary level, but the abstractions were difficult to grok. I felt that adding in thinking about more than one dimension, and thinking about abstractions in math would help my kiddo develop better math skills. If he could get used to thinking about abstractions I wasn’t exposed to until I was in my late teens, what would that do to his problem solving brain?

We would also look for array patterns around the house. We would examine Duplo and Lego bricks, muffin tins, egg cartons, game boards, crayon organizers, drink holders, watercolor paint trays… the list goes on. There are array shapes everywhere, and we would find them and discuss them. What pattern do they make? What could we call this in math or programming? Soon, kiddo was spotting array patterns himself and pointing them out. Next, I wanted to add a bit of structure to his thinking about arrays. To make things more interesting, I would ask him to identify the rows (horizontal) and the columns (vertical). We would play around with that concept. For example with an egg tray, it is natural to set it down so that it has more columns than rows, because that is how it is labeled. But what happens if we turn it so it has more rows than columns? We would identify an egg and its location: 3rd row, 2nd column, and then move the egg tray. Now it is 2nd row, 3rd column. Did the egg change, or did the “address” of the egg change? Turns out the egg is the same, but the way we describe to find that exact egg can change, depending on our perspective.

Games and Arrays

Since kiddo could easily count to 30, he could easily keep track of rows and columns in a 10×10 array. I printed out a 10×10 checkerboard and we started to play with it. I would ask him to help me determine where the rows and columns were. This took some practice, and I told him that when I was taking linear algebra in university, and then later when I worked with tables in HTML, I would remember that columns were vertical, like columns holding up a roof. Rows I remembered as horizontal, like rows on the ground in a vegetable garden. Columns hold up, rows are planted on the side. Next, we would count, making sure we kept track of the row number and the column number, which is the “address” or location in the array. Once kiddo could identify rows and columns on his own, and find a location when prompted, we started to add complexity.

I would set the checkerboard down, and ask him to locate row 2, column 3. He would take his finger, and count down to row 2, and then he would move his finger 3 spots over. While my brain was thinking of patterns in applied math, his brain was spotting a familiar pattern: games. We transitioned from counting and pointing to making simple games together. Every morning, we would take out the checkerboard, and we added in dice and game play pieces. Using dice meant I needed to expand the size of our array to 12×12. Next, for playing pieces we found Lego bricks, bingo chips, and other objects worked, but we settled on mini ring fidgets. These worked best because they weren’t associated with anything else that distracted us. From there, we would take turns rolling a single die. We both started at top left, just off of the grid, and after a roll, you would count forward to match the number on the die and move your playing piece to that position. We would move row by row from beginning to end. The first person to get to the end won.

Next, we added a die so we had a pair, and rolled both dice at once. The number on the left most die represented the row, while the next number represented the column. Instead of moving through the game board from the first column and moving through from row to row, you had to keep track of the row/column pair. This added a lot of randomization, and could cause someone who was “winning” to get knocked back. Now we were thinking and playing and having more fun. To add more randomization and surprise, kiddo would add in extra objects. If you landed on a Lego brick, you had to count the rows/columns of the brick and move to that spot on the board. If you landed on a different colored fidget ring, you had to start over. If you landed on a smiley face sticker, you could skip to the end. Now we were having a lot more fun, but it was hard to “win” because of all the randomization. To move beyond this, I added in two variations. The first was to get him to create the activities from scratch, and the second was to add in zero-based counting.

We were playing with the emerging array game every weekday morning. We would set up on the floor, and we would play around and have fun. When it started to get stale, I asked him to run the sessions. At first, I just had him tell me the rules of the game, and explain how everything worked. It was often muddled, the rules would change to favor kiddo and disadvantage dad, and the lessons about arrays were completely lost. However, I was pushing for engagement rather than mastery, so I didn’t care. On days when I ran the game, we did it according to rows and columns and reviewed what we knew about arrays. On days he led the array games, whatever happened was what was supposed to happen that day.

At first I was concerned he wasn’t taking anything away from the lessons, but when we played the game the way I had set up, he seemed to grasp the concepts more firmly. The random play was reinforcing what I was hoping he would learn. Even though he wasn’t playing by “the rules”, he was exploring the boundaries and being creative. Math lessons aside, creativity with designing your own game with dad has tremendous value on its own. It was actually reinforcing the lessons, even though it didn’t seem like it at first. He was truly owning the concept and chasing down ideas he had as things in the lesson reminded him of games we played, video games, following recipes in the kitchen, etc. There were also disagreements and lessons about playing fair, being a good sport, and other important issues. It was hard at first to not correct and bring him back to the topic at hand, but I found his brain was working on it, even if I didn’t see it at first. If I could just shut up and be a 5 year old with him in the moment, good things came out of it. I realized he was doing what I was hoping for anyway, he was applying the math. He was taking the theory and making it real.

The next variation was to make it more difficult, and to keep track of rows and columns using zero-based counting. One of my frustrations when I was programming was having to switch my brain from starting at “1” to starting at “0”. Many programming languages use zero as the first number, and I found it hard to adapt at first. When I taught adults to program later on, many also struggled with this. Instead of using your programming brain, you were expending energy trying to count to 10 starting at 0. With kiddo, I am a stickler for starting counts at zero, not one. It makes everything easier for him to have that solid grasp of zero. It helped him with place values, with counting, and it helps him with simple arithmetic. Understanding zero also helps with abstract concepts as well. Since he was familiar with starting to count with zero, and using place values to increase or decrease, transitioning from 1 to 0 based counting for arrays wasn’t that much of a stretch.

Arrays and Muffin Tins

To make this come alive, I looked for kid friendly array activities to explain this better than I could. Unfortunately, I couldn’t find anything online other than identifying arrays and looking at rows and columns. Good activities, but not what I wanted. I wanted kiddo to start thinking about arrays as an abstraction, but add the realism by keeping track of rows and columns to access something stored at each address. I wondered about a cardboard fold out activity, like a mailbox. I talked to a programmer friend, and she said her daughter had worked on a “muffin tin” math activity. Each indentation in the pan was covered with cardboard, and the kiddos would take the top off to discover items in each section of the tin. This is easy enough to do, why couldn’t I do that with arrays?

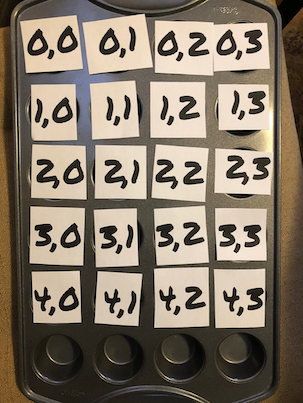
A muffin tin with paper addresses for each element in an array. It starts with 0,0 at the top left and ends with 4,3 at the bottom right.
A muffin tin set up like an array with numbers representing rows and columns.

With a bit of thought, I came up with a simple activity. I printed out slips of paper with a pair of numbers to represent the row and column, which would cover the indentations of a muffin tin. Under each address, within the muffin tin indentations, I put in a small toy. I started with Lego pieces and one Lego character. Next, I asked kiddo to find the Lego character. He needed to lift up the paper that had the row/column location, look underneath, then put it back and move on. Finally, he found the Lego character. I asked him what row and column he found the character at. Unfortunately, the location papers were scattered, so we repeated the activity, but with more care this time. To add interest, I changed the location of the character, and asked him to write down the row and column on the paper, once he had found the character again. This time, it worked. He was starting to engage. To increase engagement, I turned my back, and asked him to put the character in a new location, and then I would have to find it. He started to have fun.

Kiddo hid the Lego character at a location, and put the paper locations back on top of each indentation. Trouble was, they were out of order. Instead of pointing this out, I pointed along with my finger by moving by address, rather than physical location. Instead of starting at the top corner where 0,0 should be, I started where 0,0 actually was placed, which was somewhere else on the tin. Next I found 0,1, then 0,2 and so on. Some where in the correct location, but some were not. I feigned surprise and said I was confused. Kiddo patiently explained I should start at the top and work my way down. I suggested that if that was the case, he needed to make sure the addresses of each tin indentation was in order. He quickly shuffled the papers around so that the muffin tin rows/columns matched correctly. I then started and worked my way through until I found the Lego character.

We took turns with this activity several times, and he had lots of fun. He would try to surprise me with the location of the Lego character by putting it in the last position so I had to count all the way to the end, or at the beginning so I found it right away. He would put it back in the same location, or he would try to distract me by saying something funny while I was moving through each item. There was a lot of giggling, and when the papers with the row/column addresses got mixed up, he was quick to help sort them again.

The next day, I asked him to set up the muffin tin activity. His job was to put items in each indentation, and then put the correct address slip of paper over top, in order. We had a couple of oopses with 0,0 and 3,4, but with some clarification he remembered how it worked. This time however, we got Mom to hide the Lego character, and then we took turns trying to find it. To begin, we both started at the top left and worked our way through. The next time though, I surprised him with an algorithm. When it was my turn, I didn’t start at the beginning, I started at the end. Then I switched back to the beginning, then back again and so on. I found the Lego character first, since I was using a consistent approach. Next, I checked at the end, then the middle, and then moved back and forth from middle to end, and once again, I found the Lego character first. Kiddo was disappointed and feeling a bit frustrated that I was winning. He accused me of cheating.

This turned into a wonderful teachable moment where I could explain algorithms.

How do you explain algorithms to a 5 year old? The simplest way to describe it for him was that it was a set of steps to solve a problem. We looked at recipes for food we had prepared together, we looked at Lego instructions, and we looked at simple school assignments. Next, I explained what I was doing, that I was using a strategy called Binary search to find the Lego character faster. Since the array is small, it doesn’t give me much of an advantage, but I had lucked out by winning twice in a row. That had piqued his interest. I then explained that he had intuitively used a good algorithm, linear search, and that had worked well. He had started losing the game when he got excited and stopped concentrating. Instead of using a linear search, he was using a random search which is the least efficient. He might choose the same wrong address several times using a random search. That’s not efficient, or as effective. It is more effective and efficient (ie. find the Lego character faster) by using a consistent strategy.

A consistent strategy to solve a problem is another way to think about an algorithm. When you start to lose discipline due to emotions or getting distracted, your problem solving suffers. It’s harder to keep track, it’s easy to forget, and an opponent with a consistent approach will play better.

To reinforce the algorithm idea, we worked together on using each search algorithm. Since it is a small set of data, both linear and binary search were effective. He wanted to try binary search, so we worked together on finding logical places to divide up the data, and then work within those divisions. For example, he might look at the last address first, then look at the middle address. Next, he would move between those two addresses with each turn. He might then change tactics and try a linear search from the first address to the middle. This is a bit tricky for a young mind, because kiddo has to keep track of rows and columns, as well as the artificial divisions we were making in the grid of the array. To help keep track, we used pencils or longer Lego pieces as placeholders.

After a few days, kiddo was doing really well with the muffin tin array game. He was using a strategy to choose an algorithm, and he was comfortable with zero based counting. One day I sat back and watched him. I felt amazement and joy watching him. Not only was he demonstrating a basic understanding of arrays, but he was thinking about computer programming on his own terms. This applied math, or the “why” is absolutely crucial in learning. It was within his skill level, it was relevant to his interests, and it was fun for him.

We do programming work because kiddo has an interest in it. The TedEd Think Like a Coder series was particularly interesting to him. He had discovered this series on his own, and he looked forward to new episodes when they were released. Each episode prompted a lot of discussions about coding and me trying to replicate what they were doing in the story for him on my own PC. Sometimes I would struggle, and remembering to show him my mistakes, we would talk about how my code wasn’t working, or when I needed to look something up or ask for help from a colleague with better coding skills.

Programming is also an easy place for me to answer applied math questions, and to talk about day in the life applications of math. Sometimes the only way I can start to answer a “why do we do this” question is by working it out in code to show him an example. No, we don’t learn math for no reason at all. Yes, some people work with math every day.

Making it Real With Code

Looking at array addresses of rows and columns as zeroes felt arbitrary to kiddo. While he understood it and got it right most of the time, it really felt like one of those “grown up” things that didn’t make a lot of sense. Isn’t zero just another way to describe “nothing”? To help with this, we worked together on our home address vs. that number represented as a quantity. Next, we looked at my phone number, and then represented it as a quantity. Then we added some numbers together, which made a sum. What was different? Kiddo explained that the number in our home address and in my phone number stood for something unique, so people could find it or phone me. But a quantity was an amount of objects. A sum was calculating the total of groups of objects. We played around with this concept for a while, and stuck to the idea that an address for your house is a sort of unique label. Our neighborhood has free standing mailboxes that are labelled with a unique number that is assigned for each house address, and the contents are accessed by a key. To get the mail from another part of the world to an individual here, depends on various unique number labels.

Next, we looked at array addresses. We aren’t counting items, we are using the location in an array as a unique label. When we use zero-based counting, “0,0” is the first box in a grid. If we use one-based, “1,1” is the label. But what if we used names? How about emojis? Could we use sounds? Absolutely! We could use anything at all, really. However, number labels that follow a logical pattern work well. They are efficient and effective since they are easily understood.

To take this further, we opened up a language interpreter on my PC called irb, for the programming language Ruby. Kiddo had visited a local fish hatchery, so I typed in the following:

fish_array = ["trout", "pike", "perch"]

I explained that this was a simple array of words for fish. We read through them together I asked if he could help add in more. He suggested “walleye”, “goldeye” and “sturgeon”, so I added them to the array. We now had this array of strings, or words for fish:

fish_array = ["trout", "pike", "perch", "walleye","goldeye", "sturgeon"]

Next, I told him that I was going to use a bit of code to access the first fish in the array. I typed in:

puts fish_array[1]

and the interpreter printed this to the screen:
"pike"

“Aha! Dad! That’s not the first one!”

What do I need to do to fix it?

“You need to type ZERO, NOT ONE!”

I changed the code and tried again.

puts fish_array[0]

the interpreter printed this to the screen:
"trout"

That worked! You fixed the bug!

Kiddo really enjoyed this. We were controlling the computer, and it was important to keep track of what you were doing, because one simple error could give you the wrong answer. I explained that in computer programming, we often call this an off by one error.

We played around with this for a while, adding in array indexes that didn’t exist, to see what error would be produced. Then, I created a larger array, and used an iterator to print through each item, rather than typing in an address. Kiddo liked the idea of looping, we could do things quickly and efficiently, and you didn’t necessarily have to figure it out yourself, you could get the computer to determine what was correct for you.

We had fun. He wasn’t learning these concepts, but I was exposing him to some simple programming basics and explaining what we were doing. He had opinions and ideas about the content of arrays, and what to print out, and I would follow his lead by adding in conditionals, branching, etc. He then asked an interesting question. Essentially, he wanted to know if we could have an array that was made up of arrays. “Of course!”

I muddled around in the code to generate an array made up of arrays, and showed him how we accessed elements in an array of arrays. This started to look to him like our muffin tin game, since we needed to keep track of more than one index or address number. After a while, we had the code looping through each array within the array and printing things out, but that was getting complex and he was getting tired.

I sat back and I felt a bit shocked. Here we were, playing around with concepts I had struggled to learn when I was nineteen or twenty, and my 5 year old kiddo had grokked the basics. He could follow the form, he could play and have fun, and he understood that things could be stored in arrays, whether they were in muffin tins or mailboxes (physical), or in computer memory (virtual).

education, home school, home school math, math, modular learning, unschooling

Adventures in Homeschool: Embracing Math Mistakes

3 Comments

One issue we were struggling with in home school was overcoming the fear of getting answers wrong in mathematics. Even at five years old, kiddo’s exposure to counting heavy math activities had provoked some anxiety. He could count to 30, he could identify numbers and do simple calculations while playing games, or around the house, but in a math learning context, he would get anxious and stop engaging.

At this point in homeschooling, I was using Natural Math activities from the book Moebius Noodles by Yelena McManaman and Maria Droujkova. There were fun activities such as symmetry and mirroring, creating functions, having fun making and playing with grids, and much more. The activities were fun, math time wasn’t prone to anxiety and conflict anymore, and we were progressing. We were still at the kindergarten level so I wasn’t overly concerned that we weren’t doing math fact work or determining calculations. However, I wanted to move beyond the form and function and start helping kiddo develop number sense.

Trouble was, whenever I tried to bring in math he had been doing in preschool, he got anxious. He felt pressure to get the right answer and it stopped being fun. We had conquered the “fun” aspect of math activities, but we needed to look more explicitly at numbers and their relationships to each other. We could go through the process of solving math facts, but now we needed to talk about the facts in a non-threatening way. In short, how can we banish the anxiety kiddo feels on always needing to provide the correct answer? I looked to web discussion forums for inspiration.

Cunningham’s law describes an online phenomenon about asking for help. In essence if you want to get help online, you don’t ask the question you want answered, instead, you make an obviously false statement and wait for refutations. If you ask: “How do I do…” you won’t get much engagement. People don’t seem to want to answer direct questions, especially if they have appeared on the forum before. However, if you confidently post a wrong answer, you will get many people pointing out that you are wrong, and providing examples to show you just how wrong you are. Soon you will get the answer to your “How do you do X”, you just had to ask it in a way that people would react to and feel compelled to engage with. The xkcd comic series has a cartoon describing this obligation.

Don’t Ask a Question. State an Incorrect Answer Instead.

When I was starting out as a public speaker at software development conferences, I had a lot of anxiety. Part of it was because it was new and public speaking is hard, but part of it is because the audiences in software development can be ruthless if you get something wrong. Heckling and heated arguments can occur when you get it right, let alone if you mess something up or if you have an incorrect interpretation. At the time, software consultant Brian Marick was very kind to me and offered encouragement and advice. One tip he had was to start off with a mistake in a talk, and get it out of the way. That way you could just focus on your content and not worry about making a mistake. You’d already made the mistake, and it wasn’t so bad after all, so now focus that nervous energy in a positive way.

I found this helpful, and with experience I learned to improvise and incorporate my mistakes into the talk. If I got a fact wrong and I was corrected, I thanked the person for taking the time to help me, and corrected my materials as best I could. Mistakes weren’t so bad, and in fact, they added a richness to my corporate training. Sometimes, this was due to me getting an important detail wrong. At the time I traveled so much I would forget what city I was in, or what company I was currently at.

I also used to use incorrect answers to warm up a shy group. If I had a group that was reluctant to engage with the activities in the training, I had a secret weapon. I’d deliberately pose and then answer a question with the wrong answer, and usually someone in the audience would blurt out that it was wrong. Or at least you could see them move from surprise to chuckles, once they figured out I was doing it on purpose. People would warm up and start adding in ideas about a better solution. It also helped with groups who didn’t know each other. If they were a bit reluctant or shy to collaborate, I would break the ice by suggesting incorrect solutions, then transition to correct examples.

There seems to be an innate need for many people to correct something that is wrong. If it worked with adult learners why not try this with kids?

In the book Moebius Noodles, they discussed teaching subitizing. This is something adults have developed through working through math over a number of years, but many of us weren’t explicitly taught. I liked the idea, but I had never heard of trying to teach it before. I started reading and watching videos about how to teach my kiddo how to subitize. Trouble was, if I held up fingers or a dice or pointed to a small group of toys and asked “How many?”, the old math anxiety would flare up. The fun would stop, and kiddo would be disappointed. I felt that we could easily work from 0-6, especially since we used dice in games and he was familiar with that number range. However, instead of doing it right, I was going to do it wrong and see what happened.

I started with body mirroring activities. We stood facing each other, and I bent one arm at the elbow and held my palm facing up. Kiddo mirrored me, watching intently. Next, I adjusted my hand so I was holding up three fingers. Kiddo mirrored me, watching quietly and intently. Then I blurted out: “I am holding up FIVE fingers!” He stared at me in shock. He didn’t say anything, so I said it again. “I am holding up FIVE fingers!” He gave me a puzzled look, so I repeated myself. “I am holding up FIVE fingers!” He responded this time: “No Daddy, you’re wrong.”

I repeated myself: “I am holding up FIVE fingers!” “No Dad, that isn’t right.” I asked him what was wrong with what I was saying. “It’s wrong, you are not holding up five fingers.” He looked concerned and wasn’t sure how to proceed. This time, I started using silly voices, making faces and hamming it up. “I am holding up FIVE fingers!” Once he realized I was being silly, he started to laugh, but kept telling me it was wrong. Finally, I asked him why it was wrong. “You’re holding up three fingers.” “Pardon?” “You’re holding up three fingers.” “Pardon?” “You’re holding up THREE fingers.” He was starting to giggle now. “What? How many?” “DAD! YOU ARE BEING SILLY. YOU’RE HOLDING UP THREE FINGERS!”

Aha! Finally! Math without fear!

I then asked him to do it. He started hamming it up and holding up random numbers of fingers and deliberately stating the wrong amount. He would ham it up until I guessed and corrected him, and then we would switch. After about 5 minutes, we were doing a basic subitizing exercise that was incorporated into our mirroring activity.

This was a huge breakthrough. We hadn’t had an experience like this in weeks/months. Now we could build on this.

Wrong Answers Only

In our daily work, I started to incorporate subitizing, simple arithmetic and counting. We would use manipulatives like mathlink cubes, Lego bricks, rocks, basically anything we could use to visualize. However, we had a rule. wrong answers only! I wanted to try to get the anxiety out, and model how math should feel. It should be challenging, but it should also be fun. It should be about discovery and exploration, and the mental math and memorization will come with doing, not by being judged on your accuracy.

I deliberately chose math problems that were below his current level, and then had him come up with the wrong answers only. I could tell that he really wanted to provide the right answer, but I would delay that and remind him that we were going for wrong answers only. In fact, the reward here was for the silliest answer. After a while, he would be practically vibrating to try to correct it, and then and only then would I ask him for the correct answer.

Here were some variations:

  • Try to make me laugh, or make yourself laugh with your answers.
  • Make them sillier and sillier.
  • If they want precision, then I have a rule that there needs to be 3 silly answers first, before doing the correct one.
  • If they are tired of doing wrong answers and want to do right answers, follow their energy and switch it up.

My goal here is reframing the learning. Instead of a winner takes all, high stakes math fact question, we explore and see what happens. Instead of getting a question wrong and fixing the answer, we embrace mistakes, and to try to banish fear. Part of this approach is to get kiddo used to the format of solving problems. Part of it is to overcome anxiety and panic when posed with a math question and being expected to get the right answer, every single time. If you can get the wrong answer and the wrong answer is the correct answer, then you have the capabilities to get the correct answer when you need to provide the right answer.

Switch the Context, Gently

I wanted to tap into the knowledge he had, and to get him to demonstrate it to us, but without any anxiety or fear. I worked hard to be matter of fact and not point something out and wreck the energy of the activity.

Once we were having fun answering with only incorrect or silly answers, it was obvious that he had the capabilities to answer correctly. Once he was tiring of silliness, or if he was starting to answer with the correct answer, I would silently shift. I might verbalize this if it felt confusing, or I might just go with his energy and watch him answer correctly. I didn’t praise him for the wrong answer, or the right answer, I reacted the same way no matter what he did. I was rewarding the approach and the effort, not the answer itself.

After a while, we could do subitizing without fear. I would hold up fingers, he would answer correctly. Then I would get him to do it with me. We would take turns with fingers, dice, toys, cereal pieces, or anything else that was a small number to count. To add some variation, I started holding up 1 finger on my right hand, and 2 on my left, slowly easing in to some basic arithmetic.

If he started to freeze up or show signs of anxiety, I would ask for “wrong answers only”. If he was really starting to get wound up, we would move and work out his emotions together, and return to mathy stuff later on, or the next day. After a while, he would ask to not do silly or wrong answers, and preferred to work at providing correct answers. To keep the positive energy going, I didn’t tell him if his answers were correct until he asked me because he was curious. I was careful not to reward him for being correct only, but to reward his efforts and the process we were doing. If he got one wrong, I built up his self esteem and let him know it was ok.

Finally, we were moving out of math anxiety, and were developing a solid base we could work from. Subitizing, counting activities and simple arithmetic could be completed without anxiety, fear or conflict. This was a major step forward.

education, home school, home school math, math, modular learning, unschooling

Adventures in Homeschool: Revamping Preschool Math with Symmetry

2 Comments

In my previous posts, I wrote about issues we had with a traditional, North American approach to teaching and learning math basics. Utilizing popular approaches and activities weren’t working, so we had to try something new.

Natural Math was a lifeline for us to explore learning math with our kid. I liked the philosophy of opening up math, not putting in artificial age-based gatekeeping, that it de-emphasized counting based activities. I loved the focus on exploration, personalization of math and fun. This article, 5 Year-Olds Can Learn Calculus was an inspiration to us.

Reflection and Symmetry

One of the first activities we tried from Natural Math was body mirroring. I would stand and my son would stand opposite. I would move my right arm to a position, he would move his left arm to match me. I would extend my left leg, and he would match with his right leg. Then it was his turn. He would waggle fingers, kick a foot, or pull a funny face for me to match. Reflecting each other could easily devolve into silly giggling and fun, if someone got it wrong or did something funny

To add more variation, I also had him stand in front of a mirror and move himself, and watch carefully what happened. We would add more variation in with movement, such as moving to the side so only part of his body, or half his body was reflected. I would ask him to think like a scientist and carefully explain what he was observing. I was cautious with feedback, and I praised whatever he came up with. I also started modelling behaviour by doing it myself, and describing what I saw using different approaches. Then he would try and add more to his observations based on what he had seen me do.

My Gen Xer brain didn’t feel like this was really math, but at least he was enjoying it. I started to research reflection in mathematics to assuage my parent guilt, since I didn’t feel like I was doing a very good job in math learning.

After a few days of reflecting fun, I started to hold up a number of fingers for him to reflect as well. He would reflect different combinations of fingers on both hands with ease. I had to be careful though, if I called attention to it with: “How many fingers am I holding up”, he would get suspicious and stop having fun. I also ordered a small foldable mirror for him to play with, and once that arrived, I would put in a Lego character or a small toy, and show him the initial reflection, then fold one side in to increase the number of reflections.

Kiddo would play with that for extended periods of time, looking at things in the mirror, shifting the angle of the reflection to increase or decrease the numbers, and adding and subtracting items to add variation. It was also interesting to see what happened to an object placed in the centre, and how the object itself would get partially reflected. Reflecting half a Lego character would lead to us exploring symmetry. If you don’t get your Lego person exactly in the centre of the foldable mirror, it can reflect in unexpected ways.

Mom is an artist, and she suggested using small colorful and geometric objects to make patterns. Tangrams are fantastic items to use with a foldable mirror. He could make mandala-like reflections using tangram shapes and folding in the mirror. This led to conversations about infinite numbers, and to a topic that piqued his interest: fractals. We found videos on youtube discussing fractals, and we started to look for repeating patterns in nature. He would spot patterns in leaves, in rocks, in certain plants growing in the neighborhood or the river valley and shout out FRACTAL!

Since this was appealing to kiddo, I decided to try to tie fractals back to our reflection work, and found instructions on making a Sierpinski triangle. You draw out a large triangle on a piece of paper, find mid-points in each side of the triangle, and then draw a new triangle within the larger one. You repeat this process as many times as you can.

The Sierpinski triangle was a bit advanced for his learning at this point, and I realized we needed to look at symmetry more. Determining the line of symmetry in an object was intuitive from mirror play, but now we needed to be more explicit. I downloaded drawing and coloring worksheets to help learn more. I started with symmetry drawing exercises where a simple object would be drawn on half the paper, but at the line of symmetry, the rest of the paper would be blank and the child would need to draw it in. They would reflect the drawing in the other axes on the blank half. He found this a bit hard, so I started looking for exercises that were on a grid. The grid helped provide a guide, but the grid also had some hidden benefits. We were sneaking more math thinking we could build on later.

Counting away from the line of symmetry and then drawing a smaller part of the overall shape within that box requires more math thinking. There is counting, but now you are thinking in two dimensions. You need to keep track of rows and columns in a grid. There is counting involved, but the underpinning mathematics brings us to a matrix. Matrices lead us to arrays, and arrays lead us to different powerful abstractions for mathematics and programming. Cool!

Kiddo enjoyed working through the symmetry worksheets. We also found that the side that the drawing was on could have an effect. It was easier if the drawing was on the right side, with the left side blank, while a drawing on the left side with the blank right side left to fill in was a bit more difficult. The further away from the line of symmetry, the harder it was to get right. To get precision he was happy with counting, and keeping track of rows and columns. If he forgot, I coached him to write down the co-ordinates on his white board.

To add variation, especially when little hands get tired of drawing and coloring, we found worksheets that used the grid to make pixel-style art. He declared them to look like retro videogames or that they looked like Minecraft, and he would color in a block, rather than drawing with precision all the time. We also used bingo daubers to color in objects, as well as manipulatives like Mathlink cubes and color counting chips. These required less fine motor effort, but provided more time for variation and play.

After a few weeks, I noticed that our math time during the days was turning into a lot of fun. Instead of dreading it, or checking out when I put the math sign up to help with transitioning, he was starting to look forward to it. There was positive energy, questions, frustration with execution rather than with concepts, and he was becoming comfortable and fearless. Discussions would lead to math in real life, and he would spot symmetry in nature, or point out things around the house. Helping out with cooking and baking in the kitchen would lead to more topics for us to research and explore together.

Things were falling into place, now we needed to build on it.

education, home school, math, modular learning, unschooling

Adventures in Homeschool: Revamping Preschool Math

Leave a comment

While we were finding our way with homeschooling, our current approach to math wasn’t working. Kiddo was 5, going 6, and he had already learned a lot in preschool. He could count to 30, he could do simple arithmetic, and he could group items according to patterns. Trouble was, when I followed a lesson plan or printed off math materials, we had inconsistent results. Things started out ok, but kiddo would show signs of discomfort. He might avoid the activity by distracting, he might start the activity, then scribble all over the worksheet, or he might get upset and refuse to work on it. When we shifted to focusing on emotions and exercising to clear out the negativity, as soon as he returned to the worksheet, his mood would deteriorate. Obviously, there was something fundamentally wrong with the approach.

I came in to teaching my son predisposed with approaches that worked when I did corporate training. Some of the tools I used when teaching adults seemed appropriate for kiddos too:

  • Reward a problem solving approach rather than always getting the correct answer
  • Incorporate movement and collaboration in exercises and activities
  • Encourage productive struggle: let people figure out solutions on their own
  • Model behavior to demonstrate, then have students practice
  • Exploration, incorporating surprises or accidents, and having fun

When I started training, I was focused on knowledge and covering material, but people would get tired and bored with dense presentations, so over time I started to utilize exercises. I also got a sense of what worked well with groups and what didn’t work so well through trial and error. These were so ingrained, I found myself improvising and moving off of our daily lesson plan, when I followed the energy of my son.

I also had some unconscious biases from how I learned math as a kid:

  • Focus on correct answers rather than problem solving approaches
  • Memorizing “math facts”
  • Timed tests
  • Drills to review facts
  • Using worksheets

While I hated most of my math learning growing up, the repeated approach over twelve or thirteen years stuck with me more than I cared to admit. Furthermore, much of the math curricula and activities that I was following reinforced how I had been taught math. There were changes, such as topics such as subitizing and symmetry that were explicitly taught, rather than just picking them up as we did, but the format seemed very familiar to how I was taught. I found myself inadvertently putting pressure on my son to get the right answer on a worksheet in subtle ways. He would pick up on changes in body language, my breathing, etc. and would start to tighten up.

I decided to revamp our approach to math, and that would require some research, some hard work and retooling.

We decided to take a couple of weeks off from our homeschool kindergarten, while I researched and tried to retool. We downloaded some apps to try to help with literacy and math, and I watched to see what he liked and disliked. In the meantime I read books and searched the web for alternative approaches to teaching math to preschoolers. I didn’t come into this cold, I always knew I would need to support and enhance what he was learning in school, but I never expected to be leading the learning effort. I have taught a lot of adults how to program from my consulting and corporate training days, and there were some common problems that I had to help them overcome. Some of it was as simple as 0-based counting, and getting people to think more abstractly, rather than memorizing formulas or algorithms.

I had struggled in math and didn’t really come into my own until university, so I had a lot of thoughts about what I had missed out on in my education journey myself. I felt that my son needed to learn things I had struggled with later on, mostly because of exposure and memorizing previous “rules”. Once I was learning math in university, the approaches to learning were completely different, and I found approaches that worked well for me, but it was extremely difficult to keep up. I decided I wanted my son to have some advantages when it came to understanding:

  • zero-based counting
  • negative numbers
  • multiple dimensions (ie. arrays, grids, etc.)
  • variables (yes, letters can be numbers)
  • math can be fun.

When I was a kid, I felt this pattern when learning math. I would be taught something as a rule, only to have it change later on.

I always felt like it would have been better to teach me more of the picture, and that things were flexible, rather than absolute. For example, starting to count from 0 when looking at an array index or doing pointer math in programming was a lot of overhead at first. If I had been taught to look at 0 more often when I was younger, my brain could have spent more time on the hard parts. When I was younger, I hated how the transition to negative numbers, I felt betrayed. I was told that “2 – 3” wasn’t correct, and then all of a sudden, the rules changed. “2 – 3 == -1”. Now I had to start my math model all over. Another “rule” was that letters aren’t numbers, but then algebra came along, and that rule was cast aside. I would get extra help, go to the library and read, and find something that clicked for me, only to be told that what I actually wanted to learn was too advanced for this grade, or there wasn’t time in class. “You’ll learn that stuff later.”

This pattern repeated throughout my school career, gate keeping by age, and learning steeped in rote memorization and solving based on math facts. I suffered through timed drills, and I felt distant from the actual work. How would this apply to regular life?

It wasn’t until I was in university that math started to click for me and became fun. I even ended up in a career using applied math.

I also had a memory, from university. One of my favorite math professors was teaching his elementary aged children how to do basic linear algebra, calculus and other so-called advanced math topics. He railed against the gatekeeping we often do in elementary school curriculum. He also felt that most students weren’t taught how to think about math before they started post secondary education, and that he had to spend too much time expanding brains and getting people to move beyond memorization. The math that his kids were doing wasn’t difficult, it was just shown in a different context. His 7 year old was adding together two arrays, and the arithmetic was well within their skill level. The application of the arithmetic and keeping track of rows and columns was the challenge. However, kids love board games and can thrive with 2D arrays during play, so why not use that when learning math? You can teach abstractions and provide different contexts with basic math skills. Sadly, the book he had recommended for kids to learn more advanced topics was out of print, so I had to try to find other sources for us.

As a corporate trainer, I taught adults how to program, they were often struggling with off-by-one errors, or getting caught up in simple arithmetic because they weren’t used to starting with zero. For example, very basic programming errors could be caused by people looking at an array index, or loop counters and forgetting that they start with zero, rather than one, in many programming languages. The actual math thinking was kindergarten and first grade level, but there was often a mental block. Beyond that, looking at multi-dimensional arrays and simple algorithms or programming patterns could be extremely challenging.

It felt like a lot of people had to unlearn their approach to math first, then start learning how to actually apply the math to something in the real world. Since I had those same struggles, I could empathize and tailor my training work to help people who were having trouble learning how to program. I often thought of my old prof’s approach and wondered if there was something a bit off with how we teach math. Memorized facts don’t translate well when you are problem solving in the real world, other than to help provide a base to work from. Now, it was my responsibility to solve this problem for my son.

Finally, I found what I was looking for. Natural Math was an approach that made much more sense to me. In fact, it expanded on my thoughts of introducing him more math earlier, and emphasized fun, exploration and creativity. Unfortunately, there wasn’t a zero-prep lesson plan or worksheets I could buy and print out. There were books, lots of ideas, and different approaches and contexts I could use to create our own material.

After a couple of weeks of cramming, it was time to restart our homeschool kindergarten. We kept most of the lessons, but instead of a math worksheet or an activity with manipulatives like toys or duplo bricks, I would have him watch a video on a kindergarten math topic. I stopped using worksheets other than for topics he enjoyed to complete, such as filling in 2D graphs. He loved a particular worksheet style where he was asked to count objects, then fill in and color a bar graph based on the number of each object.

I watched him carefully, but I also had to watch myself. I could quickly ruin an otherwise positive learning experience. For example, if he made a small mistake in his graphing exercise, I would gently point out the mistake, and he would feel crushed. It would be something minor, such as him counting 5 red Duplo bricks, and then accidentally coloring in a bar graph for 6. I’d gently correct him, and the wind would go out of his sails, and a happy, smiling kiddo would look sad and start to withdraw.

The other part of my behavior I needed to adjust was to get over myself when it came to my reaction to his need to move and express himself. When he would make a connection in learning and was happy and proud of himself, he would jump up and down, flap his arms and spin. I felt that part of our homeschool work was to prepare him for learning in a classroom, so I would discourage the jumping and spinning. Once again, he would go from a happy kid who had just mastered a tricky learning problem and was full of joy to feeling shame and he would withdraw. I worked on my behavior, since what did I want him to learn? Did I want him to learn that he needed to be perfect in his math, or that he needed to master concepts and it was ok to get the wrong answer sometimes? Did I want him to sit still and stifle his emotions, or did I want him to experience joy and fun at a topic that can be challenging and many find intimidating? I decided I wanted to encourage the learning and the joy.

I decided to throw out the math resources we were using, or at least set them aside for a while and start something new. On the recommendation of the people behind Natural Math, I bought and read the book Moebius Noodles: Adventurous Math for the Playground Crowd. The hard part with Natural Math is that there are topics with examples, but there aren’t pre-free math resources you can download and start using. Instead, I read through the first chapter on symmetry, and tried the example they described in the live mirror section. To be honest, it didn’t really feel like math to me, but I was willing to try it out and see. One of the live mirror activities was to have the student stand facing you, and then you move your body, and they move to mirror it. For example, you stand with your arms at your sides, and lift your left arm and point it out from your body. They do the same thing, pretending to be your image in the mirror. For kiddo to get the hang of it, we also had him practice using a mirror first, then trying again with me.

While I didn’t feel like we were really doing math per se, the important outcome was my kiddo’s reaction. He LOVED it.

Over the next few days, we added complexity to the activity, using stuffies, toys, and other props. We tried things outside, and did more complicated movements. We even added in sequencing, where one person needed to follow 1-3 moves that the other did. We also watched videos of people dancing and doing other forms of copycat movements. The body movement and the focus on exploration, without any chance of failing to get the correct answer was a winning formula. Now we were on to something, but I needed to learn a lot more about this approach.

(to be continued…)